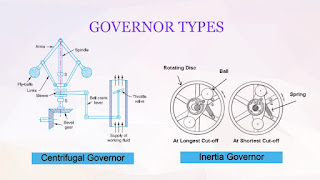
We all know that pushing down on the brake pedal slows a car to a stop. But how does this happen? How does your car transmit the force from your leg to its wheels? How does it multiply the force so that it is enough to stop something as big as a car?
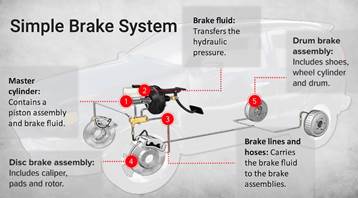
The layout of a typical brake system
When you depress your brake pedal, your car transmits the force from your foot to its brakes through a fluid. Since the actual brakes require a much greater force than you could apply with your leg, your car must also multiply the force of your foot. It does this in two ways:
· Mechanical advantage (leverage)
· Hydraulic force multiplication
The brakes transmit the force to the tires using friction, and the tires transmit that force to the road using friction as well.
Before we begin our discussion on the components of the brake system, we'll cover these three principles:
· Leverage
· Hydraulics
· Friction
Leverage and Hydraulics
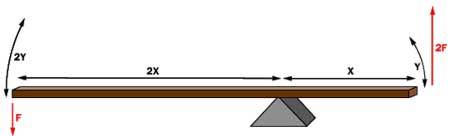
The pedal is designed in such a way that it can multiply the force from your leg several times before any force is even transmitted to the brake fluid.
In the figure above, a force F is being applied to the left end of the lever. The left end of the lever is twice as long (2X) as the right end (X). Therefore, on the right end of the lever a force of 2F is available, but it acts through half of the distance (Y) that the left end moves (2Y). Changing the relative lengths of the left and right ends of the lever changes the multipliers.
The basic idea behind any hydraulic system is very simple: Force applied at one point is transmitted to another point using an incompressible fluid, almost always an oil of some sort. Most brake systems also multiply the force in the process.
Simple hydraulic system
In the figure above, two pistons (shown in red) are fit into two glass cylinders filled with oil (shown in light blue) and connected to one another with an oil-filled pipe. If you apply a downward force to one piston (the left one, in this drawing), then the force is transmitted to the second piston through the oil in the pipe. Since oil is incompressible, the efficiency is very good -- almost all of the applied force appears at the second piston. The great thing about hydraulic systems is that the pipe connecting the two cylinders can be any length and shape, allowing it to snake through all sorts of things separating the two pistons. The pipe can also fork, so that one master cylinder can drive more than one slave cylinder if desired.
Master cylinder with two slaves
The other neat thing about a hydraulic system is that it makes force multiplication (or division) fairly easy. In a hydraulic system, all you have to do is change the size of one piston and cylinder relative to the other.
Hydraulic multiplication
To determine the multiplication factor in the figure above, start by looking at the size of the pistons. Assume that the piston on the left is 2 inches (5.08 cm) in diameter (1-inch / 2.54 cm radius), while the piston on the right is 6 inches (15.24 cm) in diameter (3-inch / 7.62 cm radius). The area of the two pistons is Pi * r2. The area of the left piston is therefore 3.14, while the area of the piston on the right is 28.26. The piston on the right is nine times larger than the piston on the left. This means that any force applied to the left-hand piston will come out nine times greater on the right-hand piston. So, if you apply a 100-pound downward force to the left piston, a 900-pound upward force will appear on the right. The only catch is that you will have to depress the left piston 9 inches (22.86 cm) to raise the right piston 1 inch (2.54 cm).
Friction
Friction is a measure of how hard it is to slide one object over another. Take a look at the figure below. Both of the blocks are made from the same material, but one is heavier. I think we all know which one will be harder for the bulldozer to push.
To understand why this is, let's take a close look at one of the blocks and the table:

Friction force versus weight
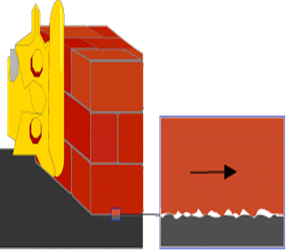
Because friction exists at the microscopic level, the amount of force it takes to move a given block is proportional to that block's weight.
Even though the blocks look smooth to the naked eye, they are actually quite rough at the microscopic level. When you set the block down on the table, the little peaks and valleys get squished together, and some of them may actually weld together. The weight of the heavier block causes it to squish together more, so it is even harder to slide.
Different materials have different microscopic structures; for instance, it is harder to slide rubber against rubber than it is to slide steel against steel. The type of material determines the coefficient of friction, the ratio of the force required to slide the block to the block's weight. If the coefficient were 1.0 in our example, then it would take 100 pounds of force to slide the 100-pound (45 kg) block, or 400 pounds (180 kg) of force to slide the 400-pound block. If the coefficient were 0.1, then it would take 10 pounds of force to slide to the 100-pound block or 40 pounds of force to slide the 400-pound block.
So the amount of force it takes to move a given block is proportional to that block's weight. The more weight, the more force required. This concept applies for devices like brakes and clutches, where a pad is pressed against a spinning disc. The more force that presses on the pad, the greater the stopping force.